| ZDD |
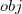 .delta(
.delta(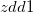 )
) 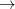
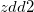
Find out the exclusive-OR (XOR) operation on 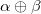 on the itemset
on the itemset 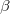 from the ZDD object
from the ZDD object 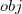 which contains
which contains  and
and 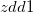 , and return the result of ZDD object as
, and return the result of ZDD object as 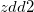 .
.
For example, XOR operations on itemset abc and bcd are as follows.
abc.delta(bcd) = abc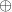 bcd = ad
bcd = ad
Find out the XOR operation between multiple itemsets.
(abc + a).delta(bcd + b) = abc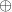 bcd + abc
bcd + abc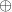 b + a
b + a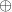 bcd + a
bcd + a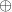 b
b
= ad + ac + abcd + ab
The weight is computed by expanding the same itemset to multiple instances.
(2abc).delta(bcd) = (abc+abc).delta(bcd) = ad + ad = 2ad
In addition, when 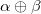 is changed to
is changed to 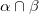 (intersection operation), it becomes delta function.
(intersection operation), it becomes delta function.
In the following, using items a,b,c, find out the exclusive OR on itemsets 2ab + a + 3b, abc + 2ab + bc + 1, ab+a.
> require 'zdd'
# First, define the itemsets
> a=ZDD::itemset("a")
> b=ZDD::itemset("b")
> c=ZDD::itemset("c")
> f=2*a*b+a+3*b
> f.show
2 a b + a + 3 b
(2ab + a + 3b)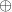 a = 3ab + 2b + 1
a = 3ab + 2b + 1
> f.delta(a).show 3 a b + 2 b + 1
(2ab + a + 3b)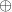 b = ab + 2a + 3
b = ab + 2a + 3
> f.delta(b).show a b + 2 a + 3
(2ab + a + 3b)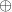 ab = 3a + b + 2
ab = 3a + b + 2
> f.delta(a*b).show 3 a + b + 2
(2ab + a + 3b)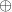 1 = 2ab+a+3b Since constant 1 is an empty itemset, it is remained in the original set for solving XOR operation.
1 = 2ab+a+3b Since constant 1 is an empty itemset, it is remained in the original set for solving XOR operation.
> f.delta(1).show 2 a b + a + 3 b
The operation result of the each term in (abc + 2ab + bc + 1)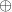 (2ab + a) are as follows:
(2ab + a) are as follows:
abc 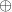 2ab = 2c
2ab = 2c
2ab 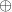 2ab = 4
2ab = 4
bc 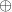 2ab = 2ac
2ab = 2ac
1 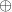 2ab = 2ab
2ab = 2ab
abc 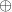 a = bc
a = bc
2ab 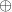 a = 2b
a = 2b
bc 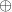 a = abc
a = abc
1 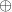 a = a
a = a
The result is summarized as a b c + 2 a b + 2 a c + a + b c + 2 b + 2 c + 4.
> g=((a*b*c)+2*(a*b)+(b*c)+1) > h=2*a*b + a > g.show a b c + 2 a b + b c + 1 > h.show 2 a b + a > g.delta(h).show a b c + 2 a b + 2 a c + a + b c + 2 b + 2 c + 4