| ZDD |
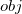 .meet(
.meet(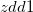 )
) 
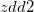
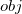 に含まれるアイテム集合
に含まれるアイテム集合 と
と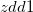 に含まれるアイテム集合
に含まれるアイテム集合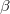 の共通集合
の共通集合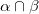 を求め、 そのZDDオブジェクト
を求め、 そのZDDオブジェクト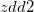 を返す。
を返す。
例えば、アイテム集合abcとbcdの共通集合は以下の通り。
 |
 |
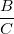 |
|||
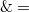 |
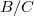 |
||||
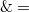 |
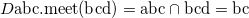 |
複数のアイテム集合間の演算では全組合せについて共通集合を求める。
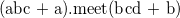 |
 |
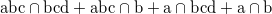 |
|||
 |
 |
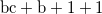 |
|||
 |
 |
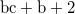 |
重みについては、同じアイテム集合を複数に展開して計算すればよい。
ちなみに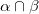 を
を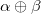 (排他的論理和演算)に変更すればdelta関数となる。
(排他的論理和演算)に変更すればdelta関数となる。
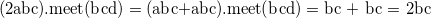 |
> require 'zdd'
> a=ZDD::itemset("a")
> b=ZDD::itemset("b")
> c=ZDD::itemset("c")
> f=a+2*a*b+3*b
# a + 2ab + 3b の各アイテム集合と引き数で指定されたアイテム集合 a との共通集合を求めると、
# a + 2a + 3 = 3 a + 3となる。
> f.meet(a).show
3 a + 3
# アイテム集合bとの共通集合を求めると 1 + 2b + 3b = 5b + 1 となる。
> f.meet(b).show
5 b + 1
# アイテム集合 ab との共通集合を求めると a + 2ab + 3b となる。
> f.meet(a*b).show
2 a b + a + 3 b
# 定数1は空のアイテム集合なので、それとの共通集合を求めると係数だけが残り 1 + 2 + 3 = 6 となる。
> f.meet(1).show
6
# abc + 2ab + bc + 1 の各アイテム集合と引き数で指定された 2ab + a の各アイテム集合との共通集合を
# 求めると、以下の通りとなる(アイテム間のスペースは省略)。
# abc ∩ 2ab = 2ab
# 2ab ∩ 2ab = 4ab
# bc ∩ 2ab = 2b
# 1 ∩ 2ab = 2
# abc ∩ a = a
# 2ab ∩ a = 2a
# bc ∩ a = 1
# 1 ∩ a = 1
# 結果をまとめると 6ab + 3a + 2b + 4 となる。
#
> f=((a*b*c)+2*(a*b)+(b*c)+1)
> g=2*a*b + a
> f.show
a b c + 2 a b + b c + 1
> g.show
2 a b + a
> f.meet(g).show
6 a b + 3 a + 2 b + 4
delta : delta演算