ZDD : ZDD演算子・メソッド一覧 : / : 除算演算子

3.7 / : 除算演算子

書式

$zdd1$ / $zdd2$ $\rightarrow$ $zdd3$

説明

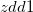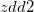
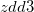
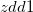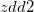$zdd1$ を $zdd2$ で除した値を計算する。詳細は以下の例に示す。

例

例1: 定数除算

重み付き積和集合xの定数cによる除算x/cは、 xの各項(アイテム集合)の重み(頻度)をcで整数除算した商を重みに持つアイテム集合が計算される。

> require 'zdd'
> a=ZDD::itemset("a")
> b=ZDD::itemset("b")
> x=13*a+3*b
> x.show
 13 a + 3 b

# aの項:13/5の商は2であるから2a。bの項:3/5の商は0であるから0bとなり表示されない。
> (x/5).show
 2 a

# aの項:13/5の余りは3であるから3a。bの項:3/5の余りは3であるから3bとなる。
> (x%5).show
 3 a + 3 b

# 除数の5に商を掛けて余りを足せば元の値xに戻る。
> (5*(x/5)+(x%5)).show
 13 a + 3 b

例2: 1つのアイテム集合による除算

重み付き積和集合xのアイテム集合vによる除算x/vは、xの各項をvで除する演算である。通常の多項式と同様に考えれば良い。

> require 'zdd'
> a=ZDD::itemset("a")
> b=ZDD::itemset("b")
> c=ZDD::itemset("c")
> x=7*a*b+5*b*c
> y=7*a*b+5*b*c+2*c
> x.show
 7 a b + 5 b c
> y.show
 7 a b + 5 b c + 2 c

# 7ab/bの商は7a。5bc/bの商は5c。
> (x/b).show
 7 a + 5 c

# 7ab/bの余りは0。5bc/bの余り0。
> (x%b).show
 0

# 7ab/3bの商は2a。5bc/3bの商は1c。2c/3bの商は0となり表示されない。
> (y/(3*b)).show
 2 a + c

# 7ab/3bの余りはab。5bc/3bの余りは2bc。2c/3bの余りは2c。
> (y%(3*b)).show
 a b + 2 b c + 2 c

# 除数の3bに商を掛けて余りを足せば元の値yに戻る。
> (3*b*(y/(3*b))+(y%(3*b))).show
 7 a b + 5 b c + 2 c

例3: 2つ以上のアイテム集合による除算

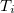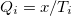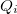2つの重み付き積和集合x,yの除算x/yは次のように計算される。除数yの各項を $T_ i$ としたとき $Q_ i=x/T_ i$ を全ての $i$ について求める。得られた $Q_ i$ 全てに共通して含まれるアイテム集合(項)について、重みの絶対値が最小の項を商Qと定義する。通常の多項式とは異なることに注意する。

> require 'zdd'
> a=ZDD::itemset("a")
> b=ZDD::itemset("b")
> c=ZDD::itemset("c")
> d=ZDD::itemset("d")

> x=2*a*b+4*a*c+a*d-2*b*c+3*b*d
> y=a+b
> x.show
 2 a b + 4 a c + a d - 2 b c + 3 b d
> y.show
 a + b

# x/yおよびx%yは以下のように計算される。
# Q1=(x/a)=2b +4c +d +0  +0  = 0  +2b +4c +d
# Q2=(x/b)=2a +0  +0 -2c +3d = 2a +0  -2c +3d
# Q1,Q2で共通のアイテム集合はcとdであり、それぞれで絶対値が最小の項は-2cとdである。
# よって求める商は以下の通りとなる。
> (x/y).show
 - 2 c + d
# x%yについてはx-(y*Q)を計算すればよい。
> (x%y).show
 2 a b + 6 a c + 2 b d

# 除数yに商を掛けて余りを足せば元の値xに戻る。
> (y*(x/y)+(x%y)).show
 2 a b + 4 a c + a d - 2 b c + 3 b d

関連

% : 剰余演算子

* : 乗算演算子