3.6 mbucket - Partition Data into Uniform Buckets

Partition numerical data field(s) specified at f= into a number of segments specified by n=. There are two ways to compute the bucket intervals. The first method is to compute an uniform spread of data points for each partition (referred to as partition of uniform buckets). The second method is to compute uniform interval ranges across partitions (referred to as partition of uniform ranges). Data is partitioned into equal interval ranges when the -rng option is specified. Otherwise, data will be partitioned uniformly across buckets if this option is not specified. When multiple fields are defined at f=, the data buckets are generated separately for each field.

Format

mbucket f= n= [-rng] [-r] [F=] [k=] [O=] [i=] [o=] [bufcount=] [-nfn] [-nfno] [-x] [-q] [precision=] [--help] [--version]

Parameters

`f=`	Partitioning is based on the value specified in this field (multiple fields can be specified).
	Target partition field name:new field name
`n=`	Number of buckets
	Specify the number of buckets to be partitioned for the field(s) defined in `f=` parameter(s).
	If 1 is defined, the command will partition by the number of items specified in `f=` parameter.
`F=`	Output format [default value: 0]
	Output format of bucket label.
	0:Display bucket numbers
	1:Display value range of buckets
	2:Display both bucket numbers and value range of buckets.
`k=`	Key field(s) to retrieve rows of data incrementally for bucket partitions (multiple keys can be specified).
`O=`	Output file with values range of bucket
	Specify output file name with values range of bucket on the field name(s) defined in parameter `f=`.
`-rng`	Define equal value of bucket range
	Divide buckets by the specified value range.
`-r`	Print bucket numbers in reverse order.

Examples

Example 1: Basic Example

Partition x and y into two subsets of equal extent and save the output file as rng.csv

$ more dat1.csv
id,x,y
A,2,7
B,6,7
C,5,6
D,7,5
E,6,4
F,1,3
G,3,3
H,4,2
I,7,2
J,2,1
$ mbucket f=x:xb,y:yb n=2 O=rng1.csv i=dat1.csv o=rsl1.csv
#END# kgbucket O=rng1.csv f=x:xb,y:yb i=dat1.csv n=2 o=rsl1.csv
$ more rsl1.csv
id,x,y,xb,yb
A,2,7,1,2
B,6,7,2,2
C,5,6,2,2
D,7,5,2,2
E,6,4,2,2
F,1,3,1,1
G,3,3,1,1
H,4,2,1,1
I,7,2,2,1
J,2,1,1,1
$ more rng1.csv
fieldName,bucketNo,rangeFrom,rangeTo
x,1,,4.5
x,2,4.5,
y,1,,3.5
y,2,3.5,

Example 2: Partition by equal range

Use -rng option to partition the data by uniform value ranges.

$ mbucket f=x:xb,y:yb n=2 -rng O=rng2.csv i=dat1.csv o=rsl2.csv
#END# kgbucket -rng O=rng2.csv f=x:xb,y:yb i=dat1.csv n=2 o=rsl2.csv
$ more rsl2.csv
id,x,y,xb,yb
A,2,7,1,2
B,6,7,2,2
C,5,6,2,2
D,7,5,2,2
E,6,4,2,2
F,1,3,1,1
G,3,3,1,1
H,4,2,2,1
I,7,2,2,1
J,2,1,1,1
$ more rng2.csv
fieldName,bucketNo,rangeFrom,rangeTo
x,1,,4
x,2,4,
y,1,,4
y,2,4,

Example 3: Example using key field

Partition x and y into two subsets of equal extent using "id" as the key parameter. By specifying n=2,3, field x is divided into 2 buckets, and field y is divided into 3 buckets. Include bucket numbers and value range of buckets in the output file (F=2).

$ more dat2.csv
id,x,y
A,2,7
A,6,7
A,5,6
B,7,5
B,6,4
B,1,3
C,3,3
C,4,2
C,7,2
C,2,1
$ mbucket k=id f=x:xb,y:yb n=2,3 F=2 i=dat2.csv o=rsl3.csv
#END# kgbucket F=2 f=x:xb,y:yb i=dat2.csv k=id n=2,3 o=rsl3.csv
$ more rsl3.csv
id%0,x,y,xb,yb
A,2,7,1:_3.5,2:6.5_
A,6,7,2:3.5_,2:6.5_
A,5,6,2:3.5_,1:_6.5
B,7,5,2:3.5_,3:4.5_
B,6,4,2:3.5_,2:3.5_4.5
B,1,3,1:_3.5,1:_3.5
C,3,3,1:_3.5,3:2.5_
C,4,2,2:3.5_,2:1.5_2.5
C,7,2,2:3.5_,2:1.5_2.5
C,2,1,1:_3.5,1:_1.5

Theorem of Arithmetic

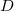Assume $D$ is a data set of n elements ( 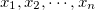$x_1,x_2,\cdots ,x_ n$ ). Partition 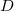$D$ uniformly into 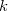$k$ number of groups (referred to as buckets) and ensure that the data is partitioned uniformly in each bucket. Dispersion is used as the fundamental evaluation criteria for uniformity.

$X=\{ x_ i~ |~ 1~ \leq ~ i~ \leq ~ n~ ,~ x_ i~ \in ~ D\}$

Arrange each value within 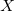$X$ in ascending order 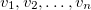$v_1,v_2,\dots ,v_ n$ . Partition of the buckets 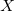$X$ is represented by partition of intervals 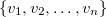$\{ v_1,v_2,\dots ,v_ n\}$ . This interval is defined as 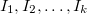$I_1,I_2,\dots ,I_ k$ . Based on these elements, 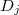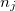$D_ j$ ? $n_ j$ , the following is defined.

$D_ j=\{ x_ i~ |~ 1~ \leq ~ i~ \leq ~ n~ ,~ x_ i~ \in ~ I_ j\}$

$n_ j=|D_ j|$

The basis of uniform dispersion is described as follows.

$Var=\sum _{j=1}^{k}~ (n_ j-\bar{n})$

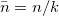If $\bar{n}=n/k$ , the equation becomes

$Var~ =~ \sum _{j=1}^{k}~ (n_ j^2-2n_ j\bar{n}+\bar{n}^2)~ ~ ~ ~ =~ \sum _{j=1}^{k}~ n_ j^2~ -~ k\bar{n}^2$

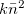$k\bar{n}^2$ remains a constant regardless of how the data is partitioned. Therefore, the first term from the above equation:

$Var’=~ \sum _{j=1}^{k}~ n_ j^2$

minimizes 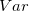$Var$ and splits the data into intervals.

Algorithm

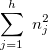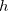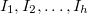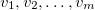Recursive equation for dynamic programming is used for optimization as illustrated in the following. The minimum value of $\displaystyle \sum _{j=1}^{h}~ n_ j^2$ is divided into $h$ intervals of $I_1,I_2,\dots ,I_ h$ of $v_1,v_2,\dots ,v_ m$ , to determine 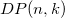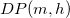$DP(n,k)$ . $DP(m,h)$ is substituted in the following function.

$DP(m,~ h)~ =~ \min _{g=h-1,~ \dots ,m-1}~ \{ ~ DP(g,h-1)~ +~ |\{ ~ x_ i~ |~ v_{g+1}~ \leq ~ x_ i~ \leq ~ v_ m~ \} |^2\}$

The above function recursively defines a sequence. Given the initial term below:

$DP(m,~ 1)~ =~ |\{ ~ x_ i~ |~ v_1~ \leq ~ x_ i~ \leq ~ v_ m~ \} |^2~ ,~ m=1,...,n$

the next term of the sequence is defined as a function of the preceding term and iterated as follows: 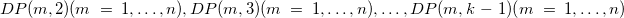$DP(m,2)(m=1,\dots ,n),DP(m,3)(m=1,\dots ,n),\dots ,DP(m,k-1)(m=1,\dots ,n)$ .

The function ends until it searches for the term 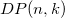$DP(n,k)$

$DP(m,~ k)~ =~ \min _{g=k-1,~ \dots ,n-1}~ \{ ~ DP(g,k-1)~ +~ |\{ ~ x_ i~ |~ v_{g+1}~ \leq ~ x_ i~ \leq ~ v_ n~ \} |^2\}$

Related command

mmbucket : Partition multidimensional data into uniform buckets