| ZDD |
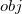 .meet(
.meet(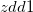 )
) 
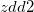
Find out the intersection 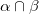 of itemsets between itemsets
of itemsets between itemsets  in
in 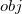 and itemsets
and itemsets 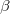 in
in 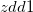 , and return as ZDD object
, and return as ZDD object 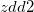 .
.
For example, the intersection of itemset abc and bcd are as follows.
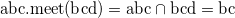 |
Find out the intersection of all combinations on multiple operations across itemsets.
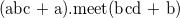 |
 |
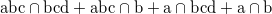 |
|||
 |
 |
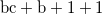 |
|||
 |
 |
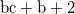 |
Weight is computed by expanding the same itemset to multiple instances.
In addition, when 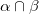 is changed to
is changed to 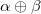 (exclusive OR operation), it becomes delta function.
(exclusive OR operation), it becomes delta function.
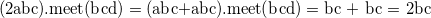 |
> require 'zdd'
> a=ZDD::itemset("a")
> b=ZDD::itemset("b")
> c=ZDD::itemset("c")
> f=a+2*a*b+3*b
# Find out the intersection of itemset a with each term in the expression a + 2ab + 3b,
# the result becomes a + 2a + 3 = 3 a + 3.
> f.meet(a).show
3 a + 3
# The intersection with itemset b becomes 1 + 2b + 3b = 5b + 1.
> f.meet(b).show
5 b + 1
# The intersection with itemset ab becomes a + 2ab + 3b.
> f.meet(a*b).show
2 a b + a + 3 b
# Empty itemset is represented by constant number 1, thus the intersection with 1
# with all coefficients becomes 1 + 2 + 3 = 6.
> f.meet(1).show
6
# Find out the interaction of each itemset in abc + 2ab + bc + 1 with each itemset
# in the specified argument 2ab + a as follows (remove space between items)
# abc ∩ 2ab = 2ab
# 2ab ∩ 2ab = 4ab
# bc ∩ 2ab = 2b
# 1 ∩ 2ab = 2
# abc ∩ a = a
# 2ab ∩ a = 2a
# bc ∩ a = 1
# 1 ∩ a = 1
# The result is summarized as 6ab + 3a + 2b + 4.
#
> f=((a*b*c)+2*(a*b)+(b*c)+1)
> g=2*a*b + a
> f.show
a b c + 2 a b + b c + 1
> g.show
2 a b + a
> f.meet(g).show
6 a b + 3 a + 2 b + 4
delta : Delta operation