| ZDD |
ここでは、これまでに紹介したZDDの各種演算を応用してNクイーン問題を解く方法を紹介する。 Nクイーン問題とは、N Nのチェス盤上 にN個のクイーンを、お互いにとられないように配置する問題である。 クイーンは将棋の飛車と角を合わせた動きのできるコマで、Figure 2.1に示されるように 上下左右と斜め4方向の計8方向に進むことができる。
Nのチェス盤上 にN個のクイーンを、お互いにとられないように配置する問題である。 クイーンは将棋の飛車と角を合わせた動きのできるコマで、Figure 2.1に示されるように 上下左右と斜め4方向の計8方向に進むことができる。
Table 2.1: "o"で示されたクイーンの動けるマス目を"x"で示している。
Table 2.2: 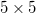 のチェス盤の座標 のチェス盤の座標
Table 2.3: 5クイーン問題の解の一例 |
5クイーン問題をZDDを用いて解くRubyスクリプトをFigure 2.1に示す。 このスクリプトで想定しているチェス盤の座標をFigure 2.2に示している。 このスクリプトの基本的な考え方は以下の通りである。 まず、クイーンを配置するマス目をアイテムと考え、 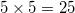 のマス目の全組み合せ、すなわち
のマス目の全組み合せ、すなわち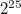 の組み合せのアイテム集合を全列挙する。 そのためには2.3節で解説した方法を使えばよい。 そして、その中から条件に合うアイテム集合を選択する。 ここで条件としては以下に示される2つを満たせば十分である。
の組み合せのアイテム集合を全列挙する。 そのためには2.3節で解説した方法を使えばよい。 そして、その中から条件に合うアイテム集合を選択する。 ここで条件としては以下に示される2つを満たせば十分である。
お互いに取られるようなアイテム集合を全て削除する。
サイズが5未満のアイテム集合を削除する。
ちなみに、サイズが5より大きいアイテム集合は、1の条件によって削除されることに注意する。 詳細は、図中にコメントとして記しているので、そちらを参考に動きを確認してもらいたい。 スクリプトの最後には、ZDDによる演算の途中で格納されたZDDオブジェクトの項の数と内部の接点数を出力している。
#!/usr/bin/env ruby
#encoding: utf-8
require "zdd"
n = 5
# 以下の二重ループにて、25マス(アイテム)の全組み合わせのアイテム集合が列挙され、変数allに格納される。
# アイテム名には座標を示した文字列"i,j"を用いている。
all=ZDD.constant(1)
(0...n).each{|i|
(0...n).each{|j|
all *= (1+ZDD::itemset("#{i},#{j}"))
}
}
# 以下で、お互いに取られる2マスの組み合せを全列挙し、変数ngに格納する。
ng=ZDD.constant(0)
(0...n).each{|i| # 行ループ
(0...n).each{|j| # 列ループ
# マス目i,jと同じ行番号(i)を持つアイテムペア
(j+1...n).each{|k|
ng+=ZDD::itemset("#{i},#{j} #{i},#{k}") # 横
}
# マス目i,jと同じ列番号(j)を持つアイテムペア
(i+1...n).each{|k|
ng+=ZDD::itemset("#{i},#{j} #{k},#{j}") # 横
}
# マス目i,jと、そこから右斜め下方向のアイテムペア
(1...[n-i,n-j].min).each{|k|
ng+=ZDD::itemset("#{i},#{j} #{i+k},#{j+k}") #
}
# マス目i,jと、そこから左斜め下方向のアイテムペア
(1...[n-i,j+1].min).each{|k|
ng+=ZDD::itemset("#{i},#{j} #{i+k},#{j-k}") #
}
}
}
st=Time.new # 時間計測用
selNG=all.restrict(ng) # 1) 全アイテム集合allからお互いに取られるアイテムペアを含むアイテム集合を選択する。
selOK=selNG.iif(0,all) # 2) 全アイテム集合allから、1)で求めたアイテム集合を除外する。
selLT=selOK.permitsym(n-1) # 3) 2)の結果から、サイズがn-1以下のアイテム集合を選択する。
ans =selLT.iif(0,selOK) # 4) 2)の結果から3)で求めたアイテム集合を除外する。
# 計算過程で作成されたZDDのアイテム集合(totalweight関数)の数、およびZDDの接点数(size関数)を表示する。
# totalweight関数はZDDの各項の重みを合計するメソッドである。
# ここでは、全ての項の重みは1なので、結果として式に含まれるアイテム集合の数が分かる。
puts "all : #{all.totalweight}\t #{all.size}"
puts "selNG : #{selNG.totalweight}\t #{selNG.size}"
puts "selOK : #{selOK.totalweight}\t #{selOK.size}"
puts "selLT : #{selLT.totalweight}\t #{selLT.size}"
puts "ans : #{ans.totalweight}\t #{ans.size}"
puts "time: #{Time.new-st}"
ans.show # 解の表示
以下に実行結果を示す。 25マスの前組み合わせは約3355万通り(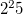 の値)と膨大であるにも関わらず、 ZDDの節点数はわずかに25である。 restrict関数によって選択されたお互いに取られる組み合わせ数(selNG)もほぼ同じ数であるが、 そのZDD節点数は587と急激に増えており、時間的にも最も時間を要するところでもある。 最終的に10のアイテム集合が解として列挙されている。 その中の最初の解(項)である"0,0 1,2 2,4 3,1 4,3"の配置をFigure 2.3に示す。
の値)と膨大であるにも関わらず、 ZDDの節点数はわずかに25である。 restrict関数によって選択されたお互いに取られる組み合わせ数(selNG)もほぼ同じ数であるが、 そのZDD節点数は587と急激に増えており、時間的にも最も時間を要するところでもある。 最終的に10のアイテム集合が解として列挙されている。 その中の最初の解(項)である"0,0 1,2 2,4 3,1 4,3"の配置をFigure 2.3に示す。
all : 33554432 25 selNG : 33553970 587 selOK : 462 193 selLT : 452 199 ans : 10 40 time: 0.003749 0,0 1,2 2,4 3,1 4,3 + 0,0 1,3 2,1 3,4 4,2 + 0,1 1,3 2,0 3,2 4,4 + 0,1 1,4 2,2 3,0 4,3 + 0,2 1,0 2,3 3,1 4,4 + 0,2 1,4 2,1 3,3 4,0 + 0,3 1,0 2,2 3,4 4,1 + 0,3 1,1 2,4 3,2 4,0 + 0,4 1,1 2,3 3,0 4,2 + 0,4 1,2 2,0 3,3 4,1
また、Nを4から10までに設定したときの、ZDDの節点数、解の数、 そして計算時間をTable 2.4に示す。 ZDDの節点数としては、全升目の全組み合わせのZDDオブジェクト(all)と、 ZDD節点数が最も多くなるZDDオブジェクト(selNG)についてのみ掲載している。 N=11でselNGの接点数が約2000万となり、1節点あたり30バイトで計算して約600Mバイトのメモリ量を消費することになる。 計算途中のワークスペースも含めて、8GBメモリのPCではN=11あたりが計算の限界となる。 ZDDを用いたより効率的な解法が文献[に示されているので、是非ともチャレンジしてもらいたい。
N |
ZDD節点数(all) |
ZDD節点数(selNG) |
解数 |
計算時間(秒) |
4 |
16 |
142 |
2 |
- |
5 |
25 |
587 |
10 |
- |
6 |
36 |
2918 |
4 |
0.017 |
7 |
49 |
15207 |
40 |
0.094 |
8 |
64 |
83962 |
92 |
0.65 |
9 |
81 |
489665 |
352 |
4.74 |
10 |
100 |
2995555 |
724 |
34.7 |
11 |
121 |
19074050 |
2680 |
247.5 |