3.6 mbucket 件数均等化バケット分割
f=で指定した数値項目をn=で指定した数の区間に分割する。 区間の計算には2通りの方法があり、一つは、 各区間に属する件数ができるだけ均等になるような区間を計算する (件数均等化バケット分割と呼ぶ)。 他方は、区間の範囲が均等になるような区間を計算する (範囲均等化バケット分割と呼ぶ)。 -rngを指定すると範囲均等分割となり、指定しなければ件数均等分割となる。 f=に複数の項目を指定した場合は、それぞれの項目ごとにバケット分割を実行する。
書式
mbucket f= n= [-rng] [-r] [F=] [k=] [O=] [i=] [o=] [bufcount=] [-assert_diffSize] [-assert_nullkey] [-assert_nullout] [-nfn] [-nfno] [-x] [-q] [tmpPath=] [precision=] [--help] [--helpl] [--version]
パラメータ
f= |
ここで指定した項目(複数項目指定可)の値に基づいて分割をおこなう。 |
分割対象の項目名:出力する項目名 |
|
n= |
分割数 |
f=で指定した項目それぞれの分割数をカンマで区切って指定する。 |
|
ただし1つの数字を指定した場合は全ての項目の分割数として扱われる。 |
|
F= |
出力形式【デフォルト値:0】 |
バケットの名前を出力形式。 |
|
0:バケット番号のみを表示する。 |
|
1:バケットの範囲のみを表示する。 |
|
2:バケット番号とバケット範囲の両方を表示する。 |
|
k= |
バケット分割を行う単位となる項目(複数項目指定可)名リスト。 |
O= |
バケット範囲出力ファイル |
f=パラメータで指定した各項目の各バケットの数値範囲を出力するファイル名。 |
|
-rng |
バケットの範囲均等指定 |
バケットの範囲が均等になるように分割する。 |
|
-r |
バケットの番号を逆順に出力する。 |
利用例
例1: 基本例
x,y項目それぞれで、件数ができるだけ均等になるように2分割する。 その際、各バケットの数値範囲をrng1.csvに出力する。
$ more dat1.csv id,x,y A,2,7 B,6,7 C,5,6 D,7,5 E,6,4 F,1,3 G,3,3 H,4,2 I,7,2 J,2,1 $ mbucket f=x:xb,y:yb n=2 O=rng1.csv i=dat1.csv o=rsl1.csv #END# kgbucket O=rng1.csv f=x:xb,y:yb i=dat1.csv n=2 o=rsl1.csv $ more rsl1.csv id,x,y,xb,yb A,2,7,1,2 B,6,7,2,2 C,5,6,2,2 D,7,5,2,2 E,6,4,2,2 F,1,3,1,1 G,3,3,1,1 H,4,2,1,1 I,7,2,2,1 J,2,1,1,1 $ more rng1.csv fieldName,bucketNo,rangeFrom,rangeTo x,1,,4.5 x,2,4.5, y,1,,3.5 y,2,3.5,
例2: 範囲均等化分割
-rngオプションを指定すると範囲均等化分割となる。
$ mbucket f=x:xb,y:yb n=2 -rng O=rng2.csv i=dat1.csv o=rsl2.csv #END# kgbucket -rng O=rng2.csv f=x:xb,y:yb i=dat1.csv n=2 o=rsl2.csv $ more rsl2.csv id,x,y,xb,yb A,2,7,1,2 B,6,7,2,2 C,5,6,2,2 D,7,5,2,2 E,6,4,2,2 F,1,3,1,1 G,3,3,1,1 H,4,2,2,1 I,7,2,2,1 J,2,1,1,1 $ more rng2.csv fieldName,bucketNo,rangeFrom,rangeTo x,1,,4 x,2,4, y,1,,4 y,2,4,
例3: キー項目を指定した例
id項目を集計キーとして、x,y項目それぞれを件数均等化バケット分割する。 n=2,3と指定することで、x項目の分割数は2に、 y項目の分割数は3となる。 出力形式はバケット番号とバケット範囲の両方を表示する(F=2)。
$ more dat2.csv id,x,y A,2,7 A,6,7 A,5,6 B,7,5 B,6,4 B,1,3 C,3,3 C,4,2 C,7,2 C,2,1 $ mbucket k=id f=x:xb,y:yb n=2,3 F=2 i=dat2.csv o=rsl3.csv #END# kgbucket F=2 f=x:xb,y:yb i=dat2.csv k=id n=2,3 o=rsl3.csv $ more rsl3.csv id%0,x,y,xb,yb A,2,7,1:_3.5,2:6.5_ A,6,7,2:3.5_,2:6.5_ A,5,6,2:3.5_,1:_6.5 B,7,5,2:3.5_,3:4.5_ B,6,4,2:3.5_,2:3.5_4.5 B,1,3,1:_3.5,1:_3.5 C,3,3,1:_3.5,3:2.5_ C,4,2,2:3.5_,2:1.5_2.5 C,7,2,2:3.5_,2:1.5_2.5 C,2,1,1:_3.5,1:_1.5
問題の定式化1
いま、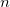 個のデータ
個のデータ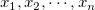 (このデータ集合を
(このデータ集合を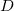 とする) が与えられている。 これらのデータを
とする) が与えられている。 これらのデータを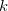 個のグループ(バケットと呼ぶ)に分割し、得られる
個のグループ(バケットと呼ぶ)に分割し、得られる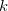 個のバケットに 入っているデータの個数が一様になるようにしたい。 一様性の評価基準としては分散を用いる。
個のバケットに 入っているデータの個数が一様になるようにしたい。 一様性の評価基準としては分散を用いる。
![\[ X=\{ x_ i~ |~ 1~ \leq ~ i~ \leq ~ n~ ,~ x_ i~ \in ~ D\} \]](images/img-0014.png) |
とおく。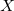 の異なる値を小さい順に並べたものを
の異なる値を小さい順に並べたものを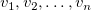 とする。
とする。 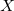 のバケット分割とは、
のバケット分割とは、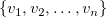 を区間に分割することを表し,その区間を、
を区間に分割することを表し,その区間を、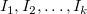 とおき、
とおき、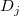 、
、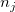 を以下のように定める。
を以下のように定める。
![\[ D_ j=\{ x_ i~ |~ 1~ \leq ~ i~ \leq ~ n~ ,~ x_ i~ \in ~ I_ j\} \]](images/img-0021.png) |
![\[ n_ j=|D_ j| \]](images/img-0022.png) |
一様さの基準である分散は以下のように定められる。
![\[ Var=\sum _{j=1}^{k}~ (n_ j-\bar{n}) \]](images/img-0023.png) |
ここで、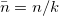 である。展開すると、
である。展開すると、
![\[ Var~ =~ \sum _{j=1}^{k}~ (n_ j^2-2n_ j\bar{n}+\bar{n}^2)~ ~ ~ ~ =~ \sum _{j=1}^{k}~ n_ j^2~ -~ k\bar{n}^2 \]](images/img-0025.png) |
となる。 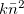 は分割の仕方によらず定数なので、
は分割の仕方によらず定数なので、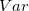 を最小化するには上式の第1項のみを考えたらよい。 つまり、
を最小化するには上式の第1項のみを考えたらよい。 つまり、
![\[ Var’=~ \sum _{j=1}^{k}~ n_ j^2 \]](images/img-0028.png) |
を最小化するような区間分割を求めることを考えたらよい。
アルゴリズム
再帰方程式を用いることによって動的計画法により解ける。詳細は以下のとおりである。 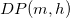 を
を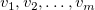 を
を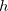 個 の区間
個 の区間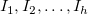 に分割したときの
に分割したときの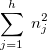 の最小値とする。 最終目標は
の最小値とする。 最終目標は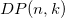 を求めることである。このとき,
を求めることである。このとき,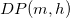 は以下の方程式を満たす。
は以下の方程式を満たす。
![\[ DP(m,~ h)~ =~ \min _{g=h-1,~ \dots ,m-1}~ \{ ~ DP(g,h-1)~ +~ |\{ ~ x_ i~ |~ v_{g+1}~ \leq ~ x_ i~ \leq ~ v_ m~ \} |^2\} \]](images/img-0035.png) |
この再帰方程式を解く。ただし,初期値は
![\[ DP(m,~ 1)~ =~ |\{ ~ x_ i~ |~ v_1~ \leq ~ x_ i~ \leq ~ v_ m~ \} |^2~ ,~ m=1,...,n \]](images/img-0036.png) |
である。再帰方程式は 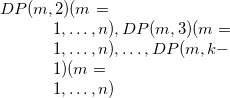 の順に解いていく。最後は,
の順に解いていく。最後は,
![\[ DP(n,~ k)~ =~ \min _{g=k-1,~ \dots ,n-1}~ \{ ~ DP(g,k-1)~ +~ |\{ ~ x_ i~ |~ v_{g+1}~ \leq ~ x_ i~ \leq ~ v_ n~ \} |^2\} \]](images/img-0038.png) |
により,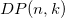 を求める
を求める
関連コマンド
mmbucket : 多次元のセルで件数均等化分割をする場合はこちらを使う。
Footnotes
- 定式化およびアルゴリズムは加藤直樹教授(京都大学工学研究科)による。