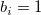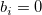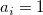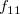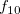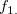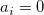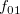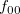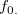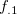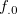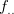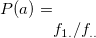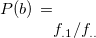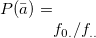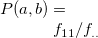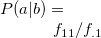3.56 msim 二変数間の類似度の計算
f=パラメータで指定した項目の二変数間の類似度(距離)を c=パラメータで指定した類似度(距離)関数で計算し類似度行列として出力する。
書式
msim c= f= [a=] [k=] [n=] [-d] [i=] [o=] [bufcount=] [-assert_diffSize] [-assert_nullkey] [-assert_nullin] [-assert_nullout] [-nfn] [-nfno] [-x] [-q] [tmpPath=] [precision=] [--help] [--helpl] [--version]
パラメータ
k= |
ここで指定された項目(複数項目指定可)を単位として求める。 |
f= |
ここで指定された項目全ての二項目間の類似度を求める。 |
c= |
類似度(距離)名リスト(複数項目指定可) |
次項に示した類似度(距離)名を指定する。 |
|
項目名は以下のように,(:)コロンに続けて指定して変更可能。 |
|
コロンに続く名称を省略した場合は類似度(距離)関数名がそのまま項目名として利用される。 |
|
例) msim f=x,y,z c=pearson:ピアソン積率相関係数,euclid:ユークリッド距離,cosine:コサイン |
|
類似度=covar|ucovar|pearson|spearman|kendall|euclid|cosine| |
|
cityblock|hamming|chi|phi|jaccard|supportr|lift|confMax| |
|
confMin|yuleQ|yuleY|kappa|oddsRatio|convMax|convMin |
|
a= |
2変数の名称を示す項目名を指定する。カンマで区切って2つ指定する。 |
省略するとfld1,fld2が使われる。 |
|
-d |
対角行列、上三角行列を出力する。 |
-dオプションが指定されないと類似度行列の下三角行列のみ出力されるが、 |
|
-dオプションを指定することにより対角行列及び上三角行列も出力される。 |
類似度(距離)の定義
実数ベクトル
サイズが同じ2つの実数ベクトル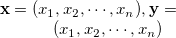 に関する類似度(もしくは距離) の定義をTable 3.24に示す。
に関する類似度(もしくは距離) の定義をTable 3.24に示す。
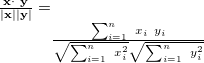
パラメータ値 内容 距離/類似度 定義式 範囲 covar 共分散 類似度 ucovar 不偏共分散 類似度 pearson ピアソンの積率相関係数 類似度 spearman スピアマンの順位相関係数 類似度 kendall ケンドールの順位相関係数 類似度 euclid ユークリッド距離(数値) 距離 cosine コサイン 類似度 cityblock 都市ブロック距離 距離 hamming ハミング距離 距離
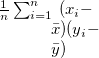
 〜
〜 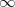
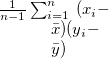
 〜
〜 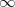
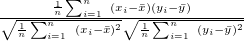
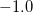 〜
〜 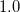
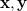 を順位に変換しての積率相関係数
を順位に変換しての積率相関係数 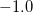 〜
〜 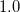
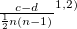
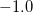 〜
〜 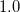
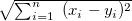
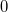 〜
〜 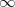
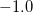 〜
〜 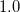
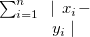
 〜
〜 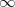
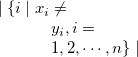
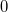 〜
〜 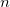
注1) 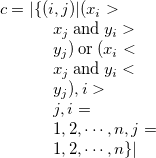
注2) 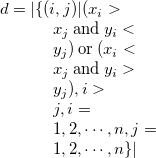
0-1ベクトル
値として0もしくは1をとる2つの0-1ベクトル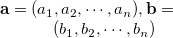 に関する類似度 の定義をTable 3.26に示す。 表の中で使われている記号
に関する類似度 の定義をTable 3.26に示す。 表の中で使われている記号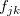 は、
は、 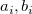 がとる値(0,1)の組み合せ別の件数で、 Table 3.25に示されている。
がとる値(0,1)の組み合せ別の件数で、 Table 3.25に示されている。
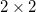 分割表
分割表 |
|
計 |
|
|
|
|
|
|
|
|
|
計 |
|
|
|
また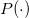 の意味は以下に示すとおりである。
の意味は以下に示すとおりである。
|
|
|
|
|
パラメータ値 内容 距離/類似度 定義式 範囲 chi カイ2乗値 類似度 phi ファイ係数 類似度 jaccard ジャックカード係数 類似度 support 支持度 類似度 lift リフト値 類似度 confMax 最大確信度 類似度 confMin 最小確信度 類似度 yuleQ yuleの連関係数(Q) 類似度 yuleY yuleの連関係数(Y) 類似度 kappa kappa 類似度 oddsRatio oddsRatio 類似度 convMax 最大conviction 類似度 convMin 最小conviction 類似度
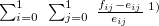
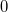 〜
〜 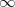
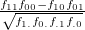
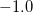 〜
〜 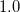
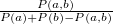
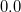 〜
〜 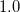
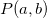
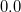 〜
〜 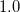
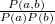
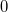 〜
〜 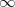
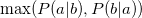
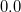 〜
〜 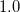
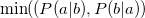
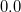 〜
〜 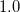
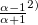
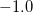 〜
〜 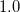
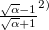
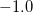 〜
〜 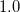
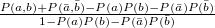
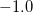 〜
〜 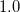
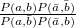
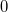 〜
〜 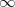
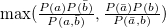
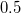 〜
〜 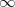
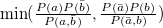
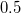 〜
〜 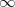
注1) 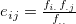 注2)
注2) 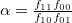
利用例
例1: 基本例
x、y、z項目の2項目間の組み合わせについて ピアソンの積率相関係数とコサインを計算する。
$ more dat1.csv x,y,z 14,0.17,-14 11,0.2,-1 32,0.15,-2 13,0.33,-2 $ msim c=pearson,cosine f=x,y,z i=dat1.csv o=rsl1.csv #END# kgsim c=pearson,cosine f=x,y,z i=dat1.csv o=rsl1.csv $ more rsl1.csv fld1,fld2,pearson,cosine x,y,-0.5088704666,0.7860308044 x,z,0.1963041929,-0.5338153343 y,z,0.3311001423,-0.5524409416
例2: 対角行列、上三角行列を出力
x、y、z項目の2項目間の組み合わせについて ピアソンの積率相関係数とコサインを計算する。(dオプションあり)
$ msim c=pearson,cosine f=x,y,z -d i=dat1.csv o=rsl2.csv #END# kgsim -d c=pearson,cosine f=x,y,z i=dat1.csv o=rsl2.csv $ more rsl2.csv fld1,fld2,pearson,cosine x,x,1,1 x,y,-0.5088704666,0.7860308044 x,z,0.1963041929,-0.5338153343 y,x,-0.5088704666,0.7860308044 y,y,1,1 y,z,0.3311001423,-0.5524409416 z,x,0.1963041929,-0.5338153343 z,y,0.3311001423,-0.5524409416 z,z,1,1
例3: キー単位での計算
key項目を単位にして計算する。
$ more dat2.csv key,x,y,z A,14,0.17,-14 A,11,0.2,-1 A,32,0.15,-2 B,13,0.33,-2 B,10,0.8,-5 B,15,0.45,-9 $ msim k=key c=pearson,cosine f=x,y,z i=dat2.csv o=rsl3.csv #END# kgsim c=pearson,cosine f=x,y,z i=dat2.csv k=key o=rsl3.csv $ more rsl3.csv key%0,fld1,fld2,pearson,cosine A,x,y,-0.8746392857,0.8472573627 A,x,z,0.3164384831,-0.521983618 A,y,z,0.1830936883,-0.6719258683 B,x,y,-0.7919009884,0.8782575583 B,x,z,-0.471446429,-0.9051543403 B,y,z,-0.1651896746,-0.8514129252
例4: 類似度名の指定
01値のデータに付いての計算。ハミング距離とphi係数を計算する。
$ more dat3.csv x,y,z 1,1,0 1,0,1 1,0,1 0,1,1 $ msim c=hamming,phi f=x,y,z i=dat3.csv o=rsl4.csv #END# kgsim c=hamming,phi f=x,y,z i=dat3.csv o=rsl4.csv $ more rsl4.csv fld1,fld2,hamming,phi x,y,0.75,-0.5773502692 x,z,0.5,-0.3333333333 y,z,0.75,-0.5773502692
例5: 類似度名の変更
01値のデータに付いての計算。ハミング距離とphi係数を計算し、 出力項目名を変更する。
$ msim c=hamming:ハミング距離,phi:ファイ係数 a=変数1,変数2 f=x,y,z i=dat3.csv o=rsl5.csv #END# kgsim a=変数1,変数2 c=hamming:ハミング距離,phi:ファイ係数 f=x,y,z i=dat3.csv o=rsl5.csv $ more rsl5.csv 変数1,変数2,ハミング距離,ファイ係数 x,y,0.75,-0.5773502692 x,z,0.5,-0.3333333333 y,z,0.75,-0.5773502692
関連コマンド
mstats : 1変量の統計量を計算するときはこちら。
mmvsim : 移動窓を設定した類似度計算。